Power function
A power function is a function where the variable \(\large x\) appears as the base with a fixed exponent.
It is written in this form:
$$ \large f(x)=k \cdot x^a $$
There are some requirements for \(\large k\) and \(\large a\):
- \(\large k \neq 0\)
- If \(\large k = 0\), the function will always give 0 in all cases, because it is multiplied by 0
- \(\large a\) can be an integer, a fraction or a negative number
- If \(\large a\) is a positive integer, you get an increasing polynomial curve
- If \(\large a\) is a fraction, you get a root function
- If \(\large a\) is negative, you get a decreasing curve similar to an inverse proportionality
If you draw a power function as a graph, it can have very different shapes depending on the exponent \(\large a\).
- \(\large a\) determines the shape and symmetry of the curve
- \(\large k\) determines how steep the curve is, and whether it points upwards or downwards
The graph can intersect the y-axis at the origin, unless a constant is added.
Exponent and intercept
\(\large a\) is called the exponent:
- If \(\large a\) is even, the curve will look like a parabola and always lie on the same side of the x-axis
- If \(\large a\) is odd, the curve will pass through the origin and have different signs in the two branches
\(\large k\) tells how steeply the curve rises or falls
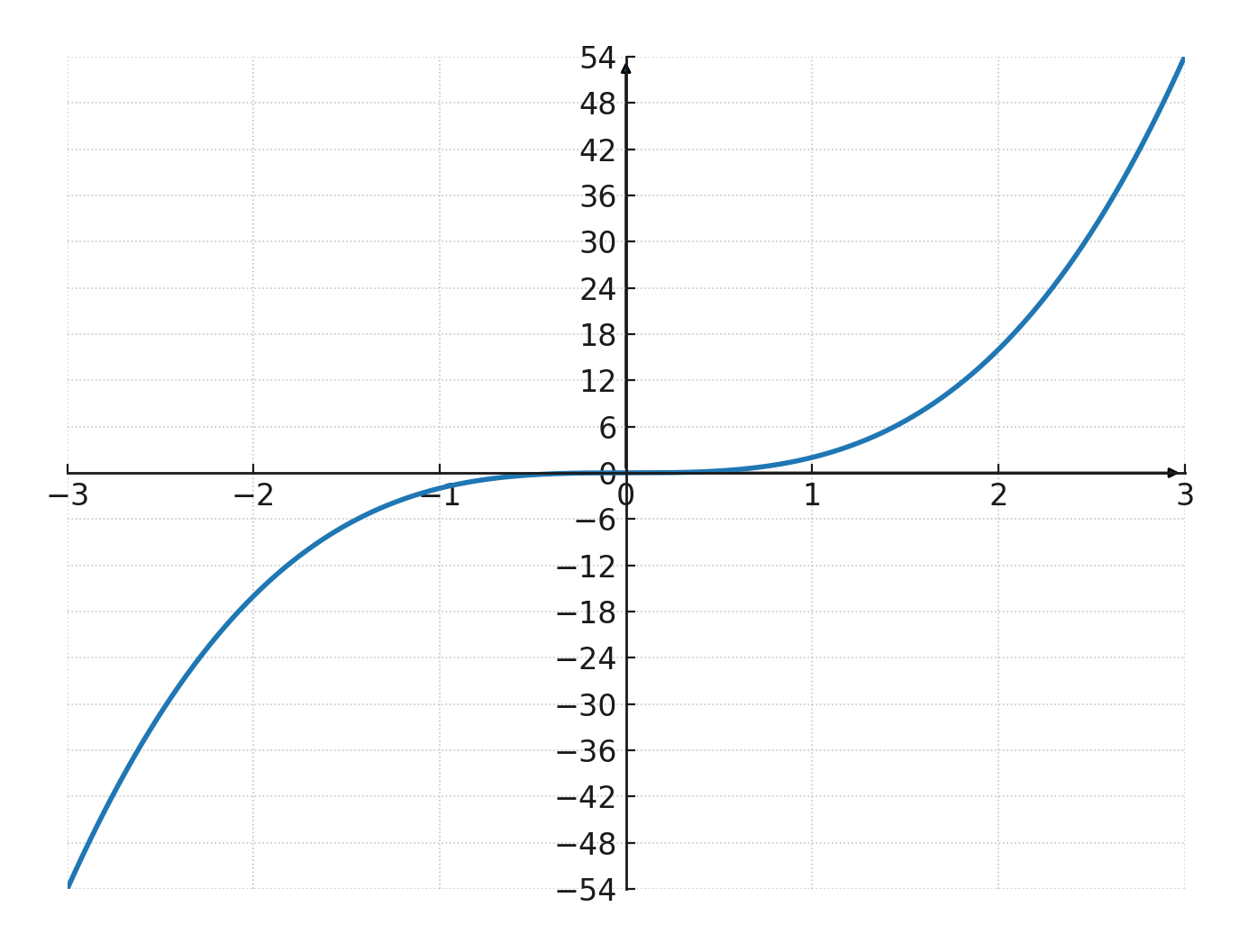
If we look at this function:
$$ \large y=2 \cdot x^3 $$
We can see that it is a power function with \(\large a=3\), which means the graph passes through the origin and is odd.
We can also see that it grows quickly, because \(\large k=2\) makes it steeper than the standard \(x^3\).
Example
We try the function \(\large y=2 \cdot x^3\)
| \(\Large x\) | -1 | -2 | -3 | 1 | 2 | 3 |
| \(\Large y\) | -2 | -16 | -54 | 2 | 16 | 54 |