Potensfunktion
En potensfunktion er en funktion hvor variablen \(\large x\) står som grundtal med en fast eksponent.
Den skrives på denne form:
$$ \large f(x)=k \cdot x^a $$
Der er nogle krav til \(\large k\) og \(\large a\):
- \(\large k \neq 0\)
- Hvis \(\large k = 0 \), vil funktionen i alle tilfælde altid give 0, fordi der ganges med 0
- \(\large a\) kan være et helt tal, et brøk-tal eller et negativt tal
- Hvis \(\large a\) er et positivt helt tal, får man en stigende polynomiumskurve
- Hvis \(\large a\) er en brøk, får man en rodfunktion
- Hvis \(\large a\) er negativ, får man en faldende kurve, der ligner en omvendt proportional
Hvis man tegner en potensfunktion som graf, kan den have meget forskellig form afhængigt af eksponenten \(\large a\).
- \(\large a\) bestemmer kurvens form og symmetri
- \(\large k\) bestemmer, hvor stejl kurven er, og om den vender opad eller nedad
Grafen kan skære y-aksen i origo, hvis ikke der er lagt en konstant til.
Eksponent og skæringspunkt
\(\large a\) kaldes for eksponenten:
- Hvis \(\large a\) er lige, vil kurven ligne en parabel og altid ligge på den samme side af x-aksen
- Hvis \(\large a\) er ulige, vil kurven gå gennem origo og have forskellig fortegn i de to grene
\(\large k\) fortæller hvor stejlt kurven stiger eller falder
Hvis vi ser på denne funktion:
$$ \large y=2 \cdot x^3 $$
Så kan vi se at det er en potensfunktion med \(\large a=3\), hvilket betyder at grafen går gennem origo og er ulige.
Vi kan også se, at den vokser hurtigt, fordi \(\large k=2\) gør den stejlere end den almindelige \(x^3\).
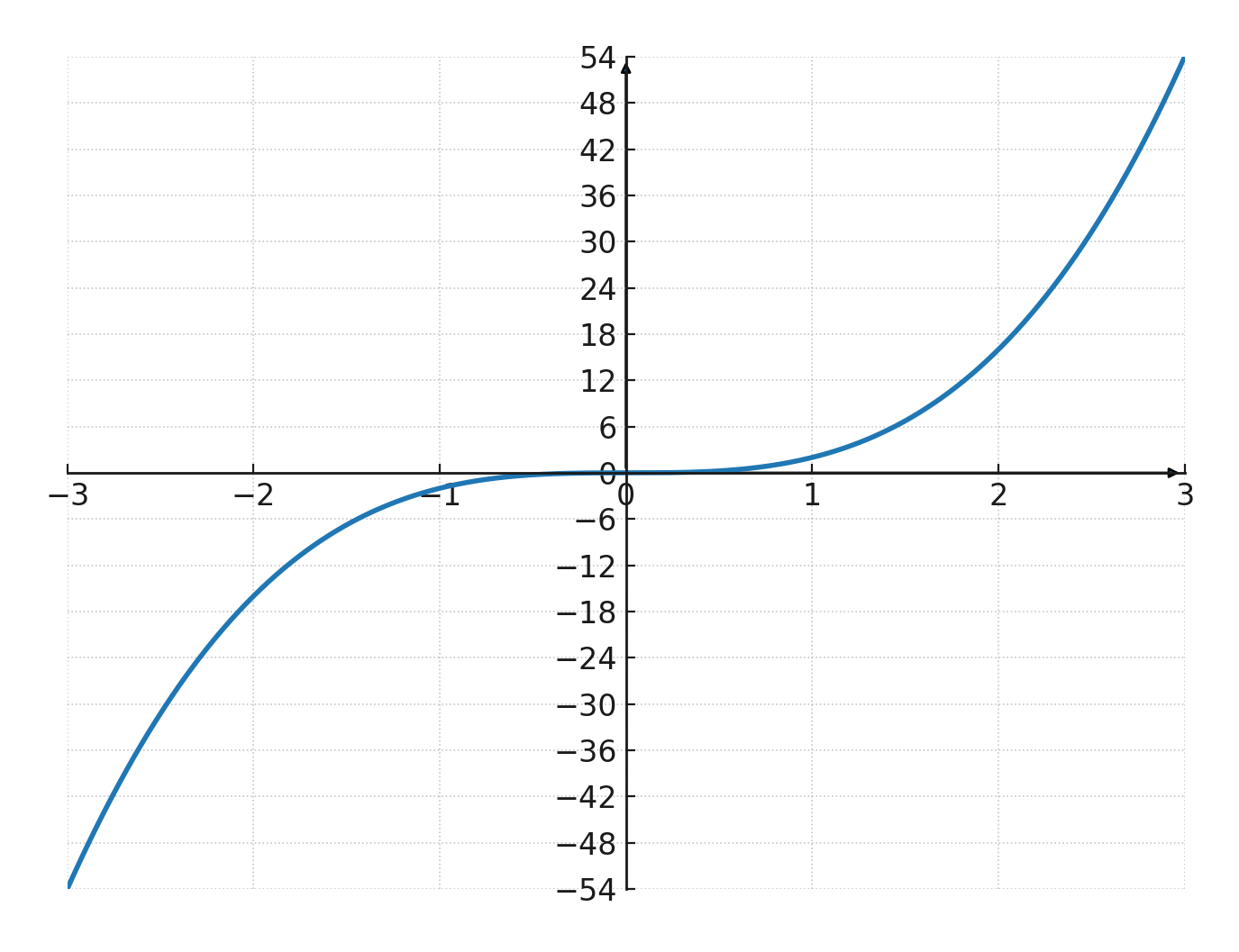
Eksempel
Vi prøver funktionen \(\large y=2 \cdot x^3\)
| \(\Large x\) | -1 | -2 | -3 | 1 | 2 | 3 |
| \(\Large y\) | -2 | -16 | -54 | 2 | 16 | 54 |