Raumgeometrie
Raumgeometrie ist der Teil der Geometrie, der sich mit Figuren im dreidimensionalen Raum beschäftigt, also mit Formen, die Breite, Höhe und Tiefe haben.
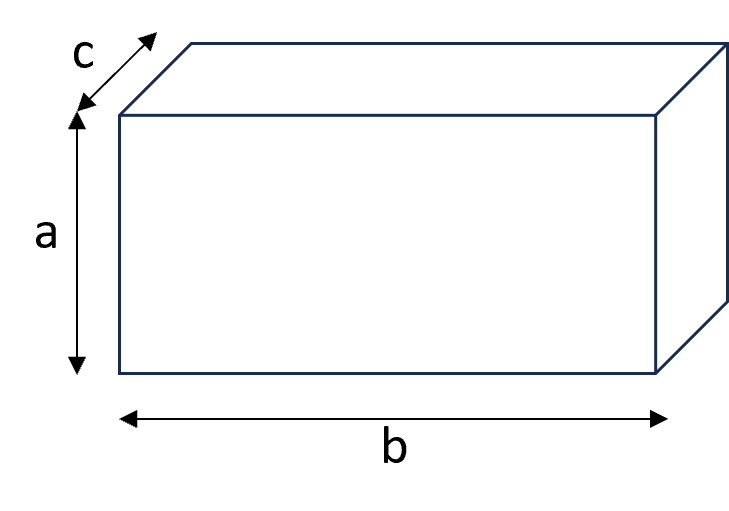
Während sich die ebenen Geometrie mit flachen Figuren befasst, arbeitet die Raumgeometrie mit räumlichen Figuren wie Würfeln, Kugeln und Pyramiden.
Raumgeometrie wird in vielen Bereichen verwendet, unter anderem in der Architektur, Physik, im Ingenieurwesen und bei 3D-Modellierungen. Sie hilft uns, räumliche Strukturen und Objekte in unserer Umgebung zu verstehen und zu berechnen.
Womit beschäftigt man sich in der Raumgeometrie?
In der Raumgeometrie untersucht man unter anderem:
- Räumliche Figuren und Körper
- Oberflächeninhalt und Volumen
- Kanten, Flächen und Ecken
- Symmetrie und Spiegelung im Raum
- Koordinaten und Lage im dreidimensionalen Raum
- Schnittpunkte zwischen Ebenen und Linien
Um räumliche Figuren zu berechnen, verwenden wir Formeln und Methoden, die die Begriffe der ebenen Geometrie auf drei Dimensionen erweitern.
Zum Beispiel verwenden wir Formeln, um das Volumen eines Würfels, den Oberflächeninhalt einer Kugel und die Diagonalen eines Prismas zu berechnen.
Beispiele für Figuren in der Raumgeometrie
Die Raumgeometrie befasst sich mit vielen verschiedenen Körperformen:
- Würfel, ein räumliches Quadrat mit sechs gleich großen quadratischen Flächen
- Prisma, eine Figur mit zwei gleichen Grundflächen und rechteckigen Seiten
- Pyramide, ein Körper mit einer Spitze und dreieckigen Seiten
- Kugel, eine vollkommen runde Figur, bei der alle Punkte gleich weit vom Mittelpunkt entfernt sind
- Zylinder und Kegel, Figuren mit gebogenen Flächen und kreisförmigen Grundflächen
Unterschied zwischen ebener und räumlicher Geometrie
Die ebene Geometrie befasst sich mit Figuren in zwei Dimensionen, wie zum Beispiel Dreiecke und Vierecke.
Die Raumgeometrie befasst sich mit Figuren in drei Dimensionen, mit Höhe, Breite und Tiefe.
Das bedeutet, dass wir in der Raumgeometrie nicht nur Längen und Fläche