Triangle isocèle
Un triangle isocèle a deux côtés de même longueur (jambes) et deux angles égaux, situés en face des deux côtés de même longueur.
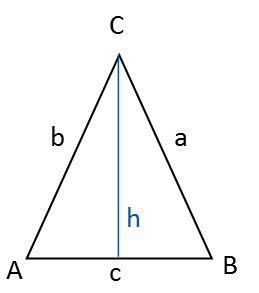
Si vous connaissez un des angles ainsi que la hauteur ou un des côtés, vous pouvez calculer les autres côtés et angles du triangle.
Conseils de calcul
Si vous connaissez un des angles, il est toujours possible de calculer les deux autres, car la somme des trois angles doit être de 180 degrés.
Si l’angle C est de 70 degrés, alors les angles A et B seront de 55 degrés, car ces deux angles sont égaux.
$$ \angle A+\angle B = 180^\circ - 70^\circ = 110^\circ \\[14pt] $$
$$ \angle A=\angle B=\frac{110^\circ}{2}=55^\circ $$
Si l’angle A est de 35 degrés, alors l’angle B est aussi de 35 degrés et l’angle C sera de 110 degrés car :
\(35+35+110=180\)
La hauteur depuis l’angle C jusqu’au côté c (opposé) divise le triangle en deux triangles rectangles symétriques. Par conséquent, vous pouvez utiliser le théorème de Pythagore et les fonctions trigonométriques pour les calculs.
Le côté c est la base du triangle et l’angle C est son sommet.