Géométrie dans l’espace
La géométrie dans l’espace est la partie de la géométrie qui étudie les figures en trois dimensions, c’est-à-dire les formes qui ont une largeur, une hauteur et une profondeur.
Alors que la géométrie plane concerne les figures plates, la géométrie dans l’espace s’intéresse aux figures en volume comme les cubes, les sphères et les pyramides.
La géométrie dans l’espace est utilisée dans de nombreux domaines, notamment en architecture, en physique, en ingénierie et en modélisation 3D. Elle nous aide à comprendre et à calculer les structures et objets dans l’espace autour de nous.
Que travaille-t-on en géométrie dans l’espace ?
En géométrie dans l’espace, on étudie entre autres :
- Les solides et les formes en volume
- Les aires de surface et les volumes
- Les arêtes, les faces et les sommets
- La symétrie et la réflexion dans l’espace
- Les coordonnées et la position dans l’espace à trois dimensions
- Les intersections entre plans et droites
Pour calculer des formes en volume, on utilise des formules et des méthodes qui prolongent les concepts de la géométrie plane en trois dimensions.
Par exemple, on utilise des formules pour calculer le volume d’un cube, l’aire de surface d’une sphère et les diagonales d’un prisme.
Exemples de figures en géométrie dans l’espace
La géométrie dans l’espace traite de nombreuses formes géométriques en volume :
- Cube, un carré spatial avec six faces carrées égales
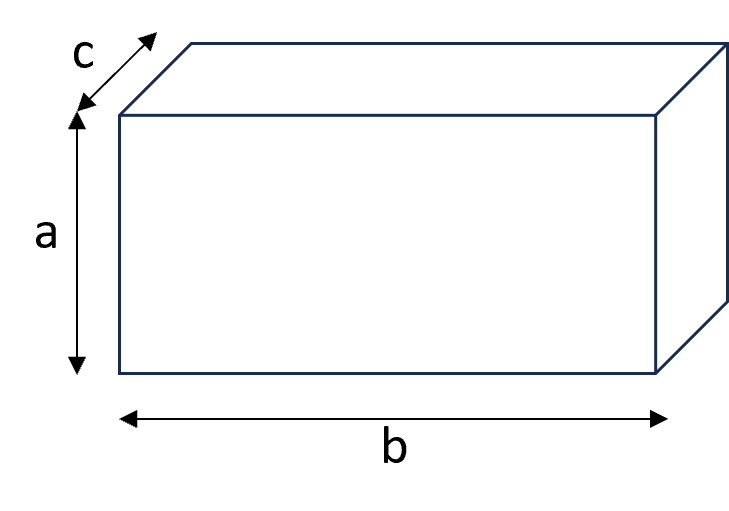
- Prisme, une figure avec deux bases identiques et des côtés rectangulaires
- Pyramide, une forme avec une pointe et des faces triangulaires
- Sphère, une figure parfaitement ronde où tous les points sont à égale distance du centre
- Cylindre et cône, formes avec des surfaces courbes et des bases circulaires
Différence entre géométrie plane et géométrie dans l’espace
La géométrie plane concerne les figures en deux dimensions, comme les triangles et les quadrilatères.
La géométrie dans l’espace concerne les figures en trois dimensions, qui ont une hauteur, une largeur et une profondeur.
Cela signifie qu’en géométrie dans l’espace, on mesure non seulement les longueurs et les aires, mais aussi le volume.
La géométrie dans l’espace prolonge la géométrie plane et permet de comprendre et de travailler avec le monde en trois dimensions.