Exponential function

An exponential function is a function where the variable \(\large x\) is in the exponent.

It is written in this form:

 

$$ \large f(x)=b \cdot a^x $$

 

There are some requirements for \(\large a\) and \(\large b\):

 

• \(\large a > 0\) and \(\large a \neq 1\)
  • If \(\large a = 1 \), the function becomes constant with no growth
  • If \(\large a \le 0\), the function cannot be calculated for all real numbers, but only for integers
• \(\large b \neq 0\)
  • If \(\large b = 0 \), the function will always be 0 in all cases, because it is multiplied by 0

 

If you draw an exponential function as a graph, it will become a steep increasing or decreasing curve.

• \(\large a\) is called the growth factor and indicates how fast the curve grows
• \(\large b\) indicates where the curve intersects the y-axis 

 

The graph will always lie on one side of the x-axis.

The x-axis acts as an asymptote, which means the curve can approach the axis but never cross it.

 

Growth factor and intercept

\(\large a\) is called the growth factor:

 

• If \(\large a>1\) the curve grows (increases)
• If \(\large a<1\) the curve decreases  

 

\(\large b\) indicates that the curve will intersect the y-axis at \(\large (0,b)\)  

 

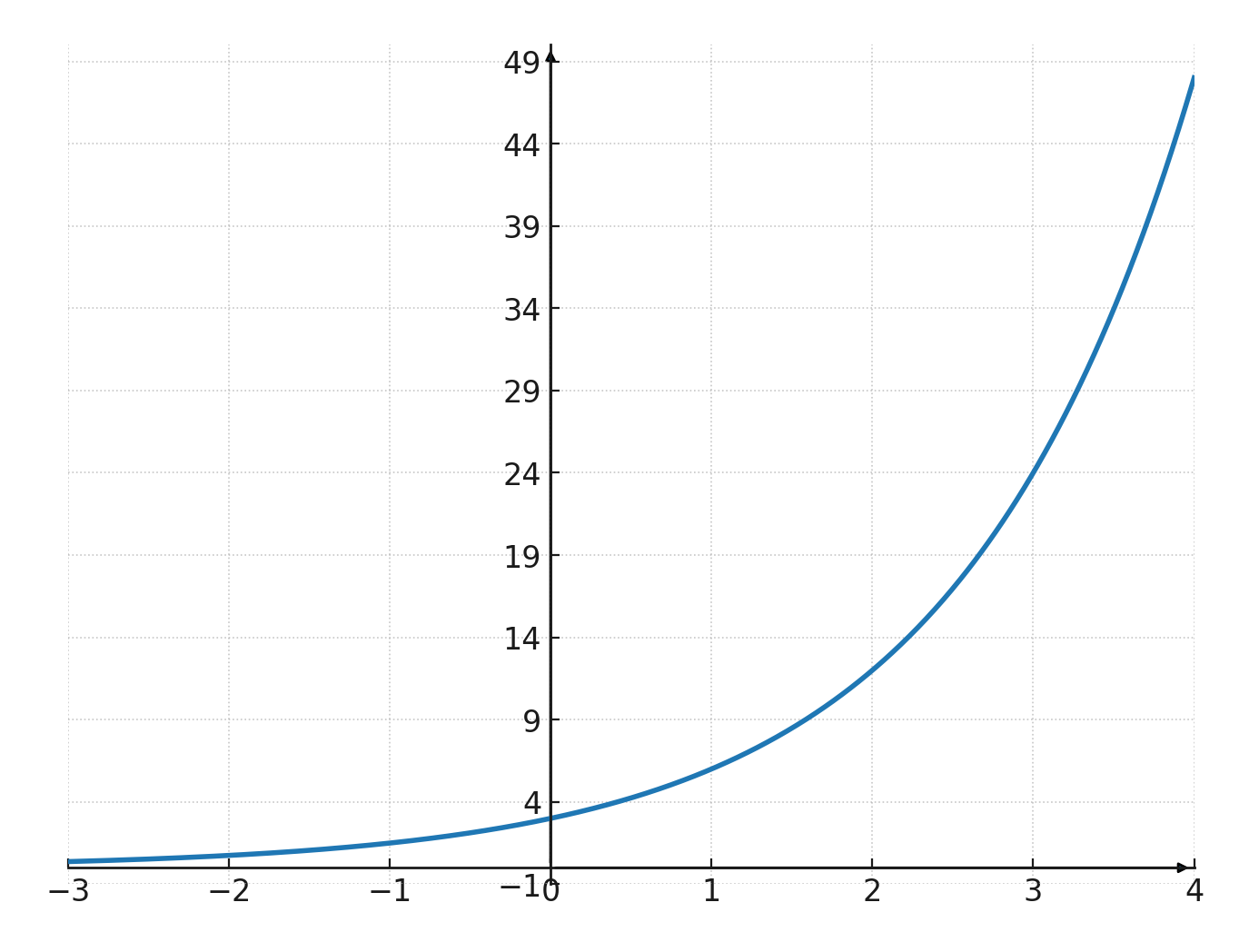
If we look at this function:

 

$$ \large y=3 \cdot 2^x $$

 

We can see that it is an increasing curve, because \(\large a=2\)

We can also see that it intersects the y-axis at \((0,3)\)

 

Example

We try the function \(\large y=3 \cdot 2^x\)

 

\(\large x\)	1	2	3
\(\large y\)	6	12	24